#CS231n #ML

Lecture 1: Introduction

约 2573 个字 6 张图片 预计阅读时间 13 分钟

简要介绍了计算机视觉的发展。

Lecture 2: Image Classification with Linear Classifiers

Image Classification 即图像分类，从一组固定的类别中为输入图像分配一个标签的任务。

Nearest Neighbor Classifier

即最近邻分类器，训练阶段几乎没有计算开销，只需存储数据，而测试的时候很慢，需要计算测试样本与所有训练样本之间的距离。
与传统的机器学习模型（如线性回归或神经网络）不同，最近邻分类器不通过训练数据提取泛化的特征或学习模型参数，而是直接依赖训练样本进行预测。这种基于实例的学习方式不符合我们对“训练模型”的传统理解，即通过训练提取通用特征以实现泛化功能。

如何比较图片的差异 ？

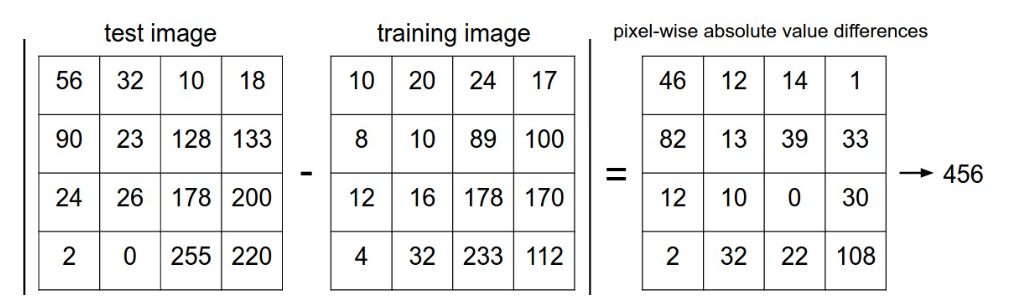
理论上图片也只是 \(w*h*channel\) ,对于 CIFAR-10 训练集 而言一张图片就是 \(32*32*3\) 个像素，对于给定的两个图片分别转换成向量 \(I_1\) 和 \(I_2\) ，差距就是：

• L1 距离（曼哈顿距离）

\[ |\mathbf{x} - \mathbf{y}|_1 = \sum_{i=1}^{n} |x_i - y_i| \]

• L2 距离（欧几里得距离）
  $$
  |\mathbf{x} - \mathbf{y}|2 = \sqrt{\sum}^{n} (x_i - y_i)^2
  $$

算法的缺陷

准确率低，往往背景或者其他非主体内容的相似会误导分类器的判断，而不是它们的语义身份，因此这种方法更多是用来引入图像分类。要真正实现图像分类需要超越原始像素。

k - Nearest Neighbor Classifier

Nearest Neighbor Classifier 是 knn 的第一种特殊情况，即 k=1，其他基本没有太大的区别

超参数 k

超参数（hyperparameter）是机器学习模型中在训练开始前需要手动设置的参数，它们不会通过训练数据的优化过程（例如梯度下降）自动学习。超参数控制模型的学习过程、结构或行为，影响模型的性能和泛化能力。可以通过交叉验证等方法来确定 k。但是交叉验证的陈本较高。

Linear Classification

相比于 knn 等方法，我们更希望通过一种新的方法来解决图像分类的问题。这种方法将有两个主要组成部分：一个将原始数据映射到类别分数的得分函数，以及一个量化预测分数和真实标签之间一致性的损失函数。然后我们将将其作为一个优化问题，在这个问题中，我们将最小化损失函数相对于得分函数参数的值。这里主要讲述的是 Linear Classification

以 CIFAR-10 为例子，它的训练集 N=50000，每张图片的维度 D 为 \(32\times 32\times 3=3072\) 有 K=10 个不同的类别。因此我们需要做的就是得到 \(f:R^D\rightarrow R^K\), 这样的一个映射函数。

以线性映射为例子：

\[ f(x_i,W,b)=Wx_i+b \]

其中 \(x_i\) 是图像展平后形如 \([D\times 1]\) 的向量，\(W\) 则是一个形如 \([K\times D]]\) 的矩阵，\(b\) 也是一个形如 \([D\times 1]\) 的向量，作为偏置向量。从而做到 3072 个输入和 10 个输出，对应十种分类的得分。

Attention

1. \(Wx_i\) 实际上是十个独立的分类器，得到十种权重
2. 我们希望的是通过训练集来调整 \(W\) 和 \(b\) ，从而使得分类器得到的正确类别的分数要高于其他错误的分数，因此学习完成后训练集就可以被丢弃了，从而使得我们可以直接通过一次矩阵乘法和加法就能够得到我们想要的结果而不是像 KNN 那样需要比较所有的测试数据

线性分类器在做什么 ？

因为我们每个图像都可以表示成一个 3072 长度的向量，因此图像可以被理解为在 3072 维度空间中的一个点，而线性分类器做的就是通过学习一组超平面（由权重 \(W\) 和偏置 \(b\) 确定），将输入空间划分为不同的区域，从而将数据点分到对应的类别。训练过程中，通过优化损失函数（例如交叉熵损失），调整超平面的参数，使其尽可能正确地区分训练样本的类别。

用一个二维图像来更好的理解：

当然线性分类器的能力太弱，很难精确匹配。

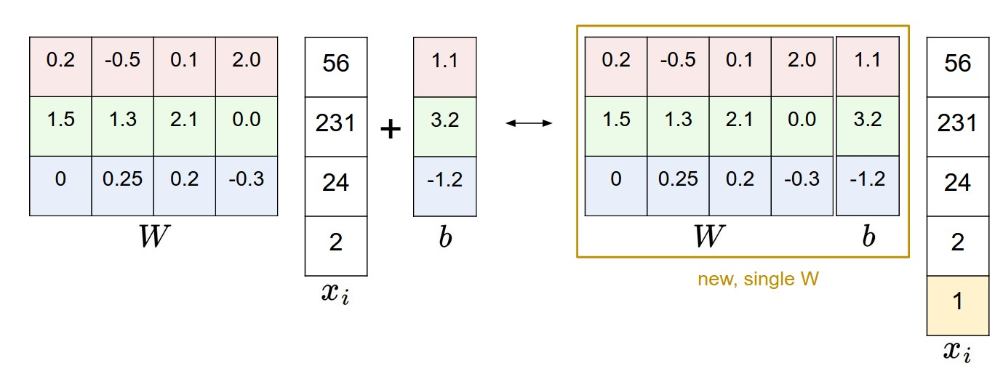
一个压缩系数的技巧

如何将 \(W\) 和 \(b\) 表示为同一个
即为 \(W\) 增加一列表示为 \(b\)，同时为 \(x_i\) 增加一个额外的常数维度 1

\[ f(x_i,W)=Wx_i \]

归一化(数据预处理)

通过让原始数据减去均值（零均值归一化）从而让像素的范围从 [0,255] 基本落在 [-127，127] 上，甚至可以进一步缩放让值的范围落在 [-1，1] ，这样做的木笔往往是让数据的有同一的分布，便于模型的训练。

损失函数

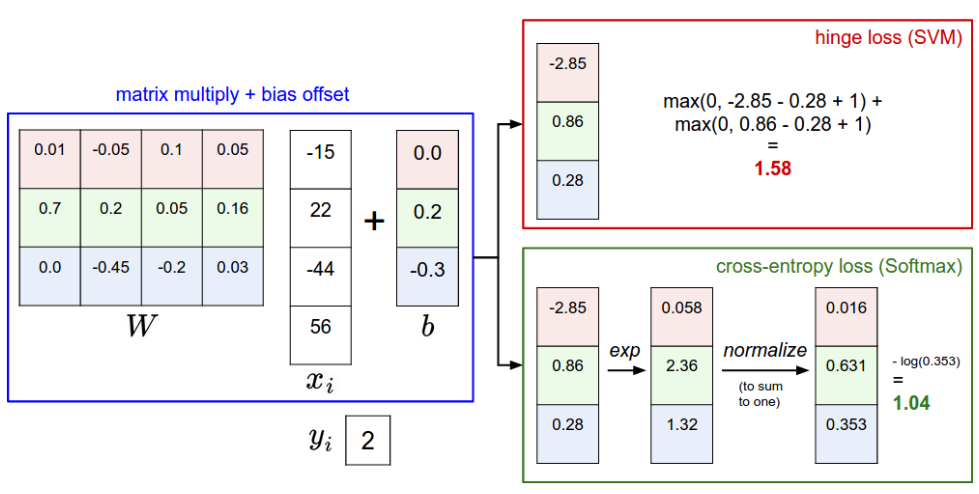
Multiclass Support Vector Machine loss

多类支持向量机损失（SVM）损失，它的定义是：

\[ L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + \Delta) \]

1. 图像的像素是表示为 \(x_i\) ，标签为 \(y_i\)
2. 令 \(s_j=f(x_i,W)_j\) 为第 j 个元素的得分向量
3. \(\Delta\) 作为一个超参数, 表示希望正确的得分 \(y_i\) 比错误的类别得分至少大 \(\Delta\)

正则化

正则化的目标是通过限制模型的复杂性，防止过拟合，提高模型的泛化能力（在新数据上的表现）。它在损失函数中引入额外的约束，平衡拟合训练数据和保持模型简单性。

举个简单的例子，上述的损失函数中的不同的 \(W\) 可能产生相同的分类记过，比如 \(W_1\) 可以，那么 \(\lambda W_1，\lambda >1\) 一定也可以。

因此我们希望加入正则化项，来惩罚 \(W\) 的复杂性。
常见的正则化有：
1. L1 正则化：

\[ R(W) = \sum_{k}\sum_{l} |W_{k,l}| \]

2. L2 正则化：

\[ R(W) = \sum_{k}\sum_{l} W_{k,l}^2 \]

经过正则化后我们的损失函数变成了这样：

\[ L = \underbrace{\frac{1}{N} \sum_i L_i}_{\text{data loss}} + \underbrace{\lambda R(W)}_{\text{regularization loss}} \]

超参数的设置

通常 \(\Delta\) 不重要，设置成 1 即可而无需交叉验证，因为正在的权衡由 \(\lambda\) 控制，通过调整 \(\lambda\) 来控制模型的复杂度和泛化能力。

Softmax classifier

本质上讲，就是将我们通 \(f\) 计算出的各种分类的得分转换成概率:

\[ P(y_i |x_i;W) = \frac{e^{f_{y_i}}}{\sum_{j} e^{f_j}} \]

相当于给定图像 \(x_i\) 和参数 \(W\) 的情况下，分配给正确标签 \(y_i\) 的概率，当然，分配给其他错误标签的概率也可以得到；
因此实际上是得到一个概率向量，表示分配给各种标签的概率：

\[ P(Y = k | x_i) = \frac{e^{f_k}}{\sum_j e^{f_j}} \]

损失函数也用交叉熵损失替换了铰链损失

交叉熵损失

交叉熵损失度量模型预测的概率分布 \(Q\) 和真实分布 \(P\) 之间的差距。在分类任务中，真实分布 \(P\) 通常是one-hot形式（正确类别为1，其余为0），而 \(Q\) 是模型通过Softmax函数计算得到的概率。

softmax 中的交叉熵损失的为：

\[ L_i = -\log P(Y = y_i | x_i) = -\log \left( \frac{e^{f_{y_i}}}{\sum_j e^{f_j}} \right) \]

这是一个推导的结果，下面我们来简单推导一下：
信息论中真实分布 \(p\) 与估计分布 \(q\) 之间的交叉熵定义为：

\[ H(P, Q) = - \sum_x P(x) \log Q(x) \]

• \(P(k)\): 真实分布 \(P\) 在类别 \(k\) 上的概率。
• \(Q(k)\): 预测分布 \(Q\) 在类别 \(k\) 上的概率。
• 意义：交叉熵表示用分布 \(Q\) 编码分布 \(P\) 所需的平均信息量

而在我们的分类任务中，真实分布 P 是一个 one-hat 类型，只有正确的一项是 1，因此：

\[ H(P, Q) = - \sum_{k=1}^C P(Y = k) \log Q(Y = k) = - \log Q(Y = y_i) = - \log P(Y = y_i | \mathbf{x}_i) \]

同时交叉熵可以被分解为：

\[ H(P,Q)=H(Q)+D_{KL}(P\|Q) \]

• \(H(P):\) 真实分布 \(P\) 的熵。
• \(D_{KL}(P\|Q)\): KL散度，衡量 \(P\) 和 \(Q\) 的差异。
• 这进一步说明，交叉熵损失的优化目标是让预测分布 \(Q\) 接近真实分布 \(P\)。

KL 散度

KL散度（Kullback-Leibler Divergence），也称为相对熵（Relative Entropy），是信息论中用来衡量两个概率分布 \(P\) 和 \(Q\) 之间差异的非对称度量。KL散度表示用分布 Q 去近似真实分布 \(P\) 时额外的信息损失。

条件：\(Q(k)=0\) 时 \(P(k)\) 必须为0，否则KL散度定义为无穷大。
离散版本的公式：

\[ D_{\text{KL}}(P \| Q) = \sum_{k=1}^C P(k) \log \left( \frac{P(k)}{Q(k)} \right)=-H(P)+H(P,Q) \]

熵的定义

熵（Entropy） \(H(P)\) 衡量分布 \(P\) 的不确定性：

\[ H(P) = - \sum_{k=1}^C P(k) \log P(k) \]

当 P 是 one-hot 分布的时候，\(H(P)=0\)，因此此时的交叉熵就是 KL 散度

SVM vs. Softmax

鲁棒性和泛化能力

• SVM：
  • 更鲁棒：只关注边际样本（接近决策边界的样本），对远离边界的样本不敏感。
  • 适合线性可分或接近线性可分的数据。
  • 在噪声数据上可能表现更好，因为不强制概率分布。
• Softmax：
  • 更敏感：对所有样本的预测概率都有贡献，即使是远离决策边界的样本。
  • 在复杂任务（如CIFAR-10）中，结合神经网络效果更好，因为可以捕捉非线性特征。

计算效率

• SVM：
  • 损失计算简单，只需比较得分差。
  • 但优化可能需要对偶形式（传统SVM）或次梯度（CS231n中的原问题形式）。
• Softmax：
  • 需要计算指数和归一化，计算开销稍大。
  • 优化更直接，梯度计算平滑。